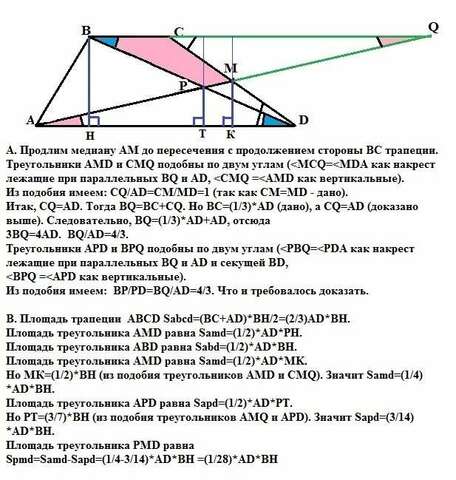
A. Продлим медиану АМ до пересечения с продолжением стороны ВС трапеции. Треугольники АМD и СMQ подобны по двум углам (Из подобия имеем: CQ/AD=СM/MD=1 (так как СМ=MD - дано).
Итак, CQ=AD. Тогда BQ=BC+CQ. Но BC=(1/3)*AD (дано), а CQ=AD (доказано выше). Следовательно, BQ=(1/3)*AD+AD, отсюда
3BQ=4AD. BQ/AD=4/3.
Треугольники АРD и ВРQ подобны по двум углам (<РВQ=<РDA как накрест лежащие при параллельных BQ и AD и секущей BD, <br><ВРQ =<AРD как вертикальные).<br>Из подобия имеем: ВР/PD=ВQ/AD=4/3. Что и требовалось доказать.
В. Площадь трапеции АВСD Sabcd=(BC+AD)*BH/2=(2/3)AD*BH.
Площадь треугольника AMD равна Samd=(1/2)*AD*PH.
Площадь треугольника ABD равна Sabd=(1/2)*AD*BH.
Площадь треугольника AMD равна Samd=(1/2)*AD*MK.
Но МК=(1/2)*ВН (из подобия треугольников AMD и CMQ). Значит Samd=(1/4)*AD*ВН.
Площадь треугольника AРD равна Saрd=(1/2)*AD*РТ.
Но РТ=(3/7)*ВН (из подобия треугольников AMQ и APD). Значит Saрd=(3/14)*AD*ВН.
Площадь треугольника РМD равна
Spmd=Samd-Sapd=(1/4-3/14)*AD*ВН =(1/28)*AD*ВН
Sbcmp=Sabcd-Sabd-Spmd=(2/3-1/2-1/28)AD*BH = (11/84)*AD*BH.
(2/3)AD*BH=56 (дано). Тогда AD*BH=84.
Sbcmp=(11/84)*84=11.