Помогите решить неравенство и объясните,пожалуйста как оно решается.

Двойное неравенство можно записать в виде системы:
$\left \{ {{x+ \frac{1}{5}\ \textless \ -0,2} \atop {x+ \frac{1}{5}\ \textgreater \ -2x^2}} \right.$
решим каждое неравенство по отдельности:
$x+ \frac{1}{5}\ \textless \ -0,2 \\5x+1\ \textless \ -1 \\5x\ \textless \ -2 \\x\ \textless \ - \frac{2}{5} \\x\ \textless \ - 0,4 \\x \in (-\infty;-0,4)$
$x+ \frac{1}{5}\ \textgreater \ -2x^2 \\5x+1\ \textgreater \ -10x^2 \\10x^2+5x+1\ \textgreater \ 0 \\D=25-40\ \textless \ 0$
так как D<0, то данное неравенство не имеет корней, но 10>0 => у параболы ветви направленны вверх => парабола лежит выше оси ox и принимает всегда положительные значения, то есть $x \in R$
теперь пересекаем множества решений этих двух неравенств:
$x\in (-\infty;-0,4)\cap R=(-\infty;-0,4)$
Ответ: $x \in (-\infty;-0,4)$

Чтобы решить двойное неравенство, нужно разложить его на два неравенства по проще:
1) x+1/5>-2x^2
2) x+1/5<-0,2<br>То есть это то же самое, только в другом виде. Теперь решим.
1) x+1/5+2x^2>0
Приводим к общему знаменателю
5x+1+10x^2>0
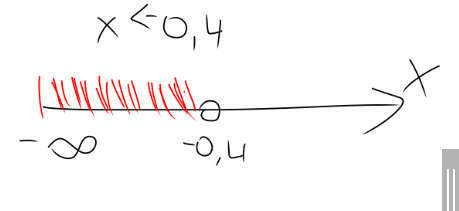
У квадратного уравнения D<0, решений нет, но мы смотрим на коэффициент “a”, если он больше 0, значит x€R (любое число)<br>2) x<-0,4<br>Отметим на числовой оси для удобства определения интервалов.
Ответ в неравенствах всегда записывается каким то промежутком. Здесь он: (-∞; -0,4)