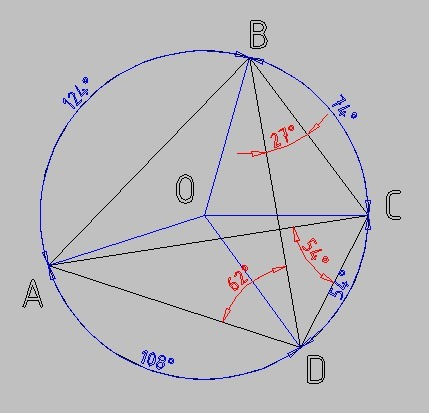
О - центр окружности
Три данных по условию вписанных угла изображены на рисунке красным.
Соответствующие им центральные углы в два раза больше.
∠CBD = 27° ⇒ ∠CОD = 54°
∠ACD = 54° ⇒ ∠AОD = 108°
∠ADB = 62° ⇒ ∠AОB = 124°
Сумма всех центральных углов вокруг точки О равна 360°, и это поможет нам найти четвёртый центральный угол ∠ВОС
∠ВОС = 360°-54°-108°-124° = 74°
Теперь можно найти углы четырёхугольника, снова учитывая, что вписанный угол в два раза меньше центрального, опирающегося на ту же дугу.
∠ABC = 1/2(108+54) = 54+27 = 81°
∠BCD = 1/2(108+124) = 54+62 = 116°
∠CDA = 1/2(124+74) = 62+37 = 99°
∠DAB = 1/2(74+54) = 37+27 = 64°