|x² - 9|(x² + 2x - 8) ≤ 0
Так как модуль всегда неотрицательный, то решение неравенства разбивается на две части
1) |x² - 9| = 0
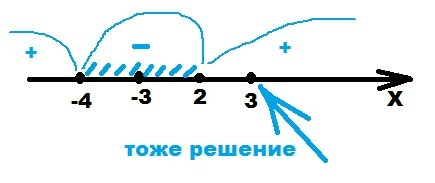
x² = 9 ⇒ x₁ = 3; x₂ = -3
2) x² + 2x - 8 ≤ 0
D = 4 + 4·8 = 36 = 6²

x₃ = -4; x₄ = 2
x² + 2x - 8 ≤ 0 ⇔ (x + 4)(x - 2) ≤ 0
Решение на числовой прямой
x ∈ [-4; 2]
Ответ: x ∈ [-4; 2] ∪ {3}