Кривая задана уравнением Р=Р(ф) (фи) в полярной системе координат.

$\rho=\frac{1}{2-cos\phi}$
1. Найдем область определения
$\rho \geq 0 \Rightarrow 2-cos\phi \ \textgreater \ 0 \Rightarrow cos\phi\ \textless \ 2$
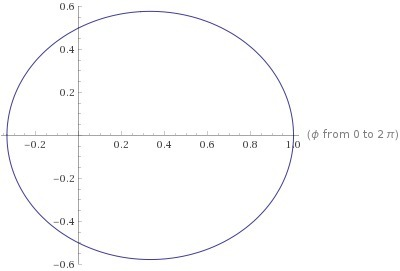
Следовательно, φ может принимать любые значения. Построение кривой в полярной системе координат дает эллипс (см. прикрепленный файл)
2. Найдем каноническое уравнение кривой в ПСК
$\rho=\frac{1}{2-\cos\phi} \Rightarrow \rho(2-\cos\phi)=1 \Rightarrow 2\rho-\rho\cos\phi=1$
Зная, что
$\left \{ {{x=\rho\cos\phi} \atop {y=\rho\sin\phi}} \right.$
и
$\rho= \sqrt{x^{2}+y^{2}}$
получим
$2\sqrt{x^{2}+y^{2}}-x=1\\ (2\sqrt{x^{2}+y^{2}})^2=(x+1)^2\\ 4(x^{2}+y^{2})=x^{2}+2x+1\\ 3x^{2}-2x+4y^{2}=1\\ 3(x^2-\frac{2}{3}x+\frac{1}{9})-\frac{1}{3}+4y^2=1\\ 3(x-\frac{1}{3})^{2}+4y^2=\frac{4}{3}\\ \frac{(x-\frac{1}{3})^{2}}{\frac{4}{9}}+\frac{y^2}{\frac{1}{3}}=1\\ \frac{(x-\frac{1}{3})^{2}}{(\frac{2}{3})^{2}}+\frac{y^2}{(\frac{1}{\sqrt3})^{2}}=1\\$
Последняя запись - уравнение эллипса в прямоугольных координатах в каноническом виде с центром в точке $O(\frac{1}{3};0)$ , большой полуосью $a=\frac{2}{3}$ и малой полуосью $b=\frac{1}{\sqrt 3}$ . По этим данным самостоятельно построить эллипс в ПСК сложности не составит.
Остальные задания делаются по аналогии.