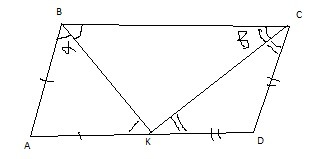
Пусть К - точка пересечения биссектрис ВК и СК, К∈AD
∠ABK=∠KBC=α, ∠BCK=∠KCD=β.
∠ВСК=∠CKD=β как накрест лежащие при пересечении BC||AD секущей CK.
∠KBC=∠BKA=α как накрест лежащие при пересечении BC||AD секущей BK.
∠ABK = ∠AKB=α => ABK равнобедренный, AB=AK.
∠CKD=∠DCK=β => KCD равнобедренный, KD=CD
AD=AK+KD=AB+CD=2AB
P=2(AB+AD)=6AB
6AB=18, AB=3(см).
AD=3*2=6(см).
Ответ: AD=BC=6 см, AB=CD=3 см.