Длина хорды:
l= d*sin(a/2),
где d - диаметр, a - центральный угол, опирающийся на хорду.
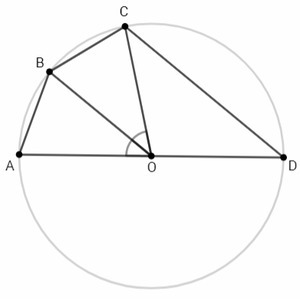
AB=AD*sin(∠AOB/2) <=> sin(∠AOB/2)= AB/AD =1/3
∠AOB=∠BOC (центральные углы, опирающиеся на равные хорды)
∠COD/2= (180-∠AOC)/2 =90-∠AOB
sin(∠COD/2) =sin(90 -∠AOB) =cos(∠AOB)
Синус половинного угла:
sin^2(a/2)= [1-cos(a)]/2
cos(∠AOB)= 1 -2sin^2(∠AOB/2) =1 -2/9 =7/9
CD=AD*sin(∠COD/2) =3*7/9 =7/3
ИЛИ
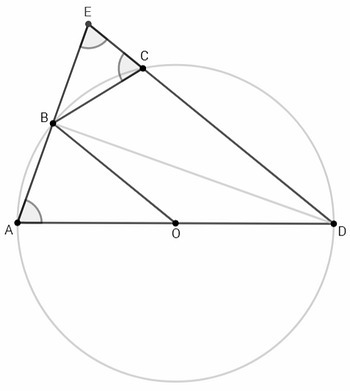
На продолжении AB построим отрезок BE равный AB.
В треугольнике ADE отрезок DB является медианой (AB=BE) и биссектрисой (вписанные углы ADB и EDB опираются на равные хорды AB и BC) => △ADE - равнобедренный => ∠A=∠E
△BCE - равнобедренный (BE=BC=1) => ∠E=∠BCE => △ADE~△BCE, коэффициент подобия k=AD/BC=3
AE=2AB=2
EC=AE/k =2/3
ED=AD=3
CD=ED-EC =3 -2/3 =7/3