Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.
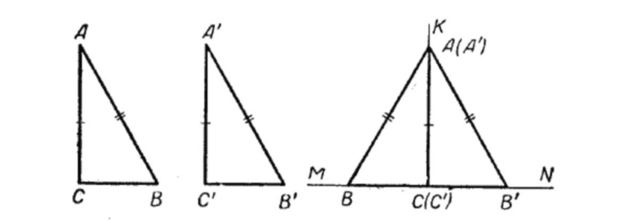
Чтобы доказать это, построим два прямоугольных треугольника АВС и А’В’С’, у которых углы С и С’ — прямые, катеты АС и A’C’ равны, гипотенузы АВ и А’В’ также равны
Проведём прямую MN и отметим на ней точку С, из этой точки проведём перпендикуляр СК к прямой MN. Затем прямой угол треугольника ABC наложим на прямой угол КСМ так, чтобы вершины их совместились и катет АС пошёл по лучу СК, тогда катет ВС пойдёт по лучу СМ. Прямой угол треугольника А’В’С’ наложим на прямой угол KCN так, чтобы вершины их совместились и катет А’С’ пошёл по лучу СК, тогда катет С’В’ пойдёт по лучу CN. Вершины А и А’ совпадут вследствие равенства катетов АС и А’С’.
Треугольники АВС и А’В’С’ составят вместе равнобедренный треугольник ВАВ’, в котором АС окажется высотой и биссектрисой, а значит и осью симметрии треугольника ВАВ’. Из этого следует, что Δ
ΔАВС = ΔА’В’С’.