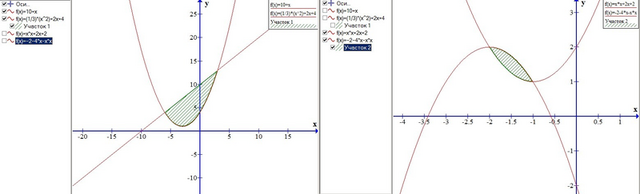
1) Найдем точки пересечения графиков:
(1/3)*x^2+2x+4 = 10+x
(1/3)*x^2 + x - 6 = 0 | * 3
xx + 3x - 18 = 0
D = 9 + 4*18 = 81
x1, 2 = (-3+-9)/2
x1 = -6
x2 = 3
Далее нужно найти определенный интеграл A от 10+x при х от -6 до 3, определенный интеграл B от 1/3x^2+2x+4 при х от -6 до 3, их разность и будет искомой площадью фигуры:
Интеграл (1/3)*x^2+2x+4 = x*x*x/9 + x*x + 4x + C
(3 + 9 + 12) - (-24 + 36 - 24) = 24 + 12 = 36
Интеграл 10+x = x*x/2 + 10x + C
36/2 - 60 = -42
3*3/2+30 + 42 = 76,5
76,5 - 36 = 40,5
Ответ: 40.5 кв. ед.
2) В условии небольшая ошибка, -2 - 4 - x^2 следует понимать как -2 - 4x - x^2, иначе решений нет, т. к. площадь пересечения равна нулю.
Найдем точки пересечения:
x^2 + 2x + 2 = -2 - 4x - x^2
2x^2 + 6х + 4 = 0
хх + 3х + 2 = 0
В = 9 - 8 = 1
x1,2 = (-3 +- 1)/2
x1 = -2
x2 = -1
График функции -2-4*x-x*x находится выше.
Неопределенный интеграл от -2-4*x-x*x равен -2x - 2x*x - x*x*x/3 + C.
При х = -1: 2 - 2 + 1/3 = 1/3.
При х = -2: 4 - 8 + 8/3 = -4 + 8/3
1/3 - (-4 + 8/3) = 4 - 7/3 = 5/3.
Неопределенный интеграл от x^2+2x+2 равен х*х*х/3 + х*х + 2х + С.
При х = -1: -1/3 + 1 - 2 = -1/3 - 1.
При х = -2: -8/3 + 4 - 4 = -8/3
-1/3 - 1 + 8/3 = 7/3 - 3/3 = 4/3
5/3 - 4/3 = 1/3
Ответ: 1/3 кв. ед.