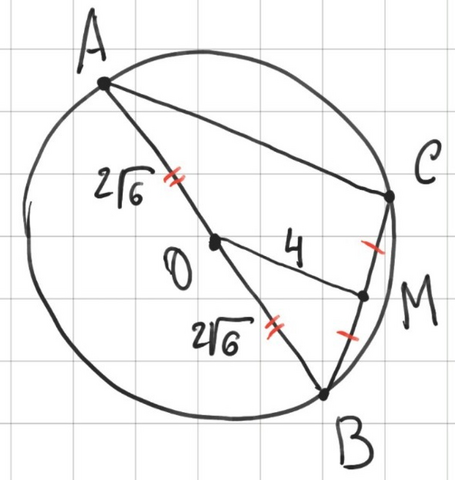
Дан радиус 2√6. Радиус равен половине диаметра. Так как АО и ОВ - радиусы, они равны. Находим диаметр:
АВ = r * 2 = 2√6 * 2 = 4√6
По условию, точка М является серединой СВ. Точка О является центром окружности и серединой диаметра АВ соответственно. Получается, отрезок ОМ проходит через середины сторон ΔАВС, а значит, является его средней линией.
Средняя линия треугольника в два раза меньше его основания. Отсюда:
АС = ОМ * 2 = 4 * 2 = 8
Существует теорема, что если гипотенуза треугольника опирается на диаметр окружности, то такой треугольник - прямоугольный. Отсюда ∠С = 90°.
Мы знаем катет и гипотенузу ΔАВС. По теореме Пифагора находим второй катет, обозначив неизвестный за х:
х² + 8² = (4√6)²
х² + 64 = 96
х² = 32
х = 4√2