Только что была такая же задача, из другого варианта.
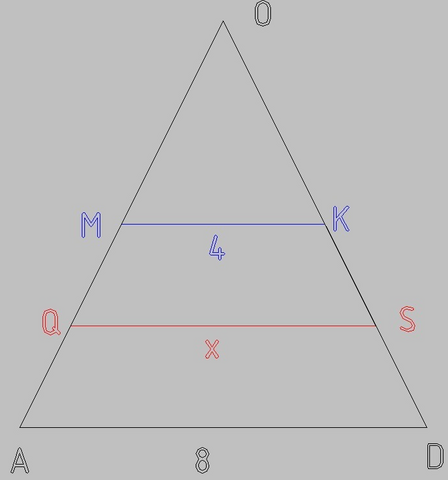
Т.к. пирамида правильная, то в основании квадрат, все стороны которого равны 8
Т.к. МК соединяет середины сторон BS и CS треугольника BCS, то МК - это средняя линия, и её длина равна половине длины стороны BC
МК = BC/2 = 8/2 = 4
Рассечём пирамиду плоскостью, проходящей через ребро AD и отрезок MK
Треугольники ОМК и ОАD подобны с коэффициентом подобия 2, если принять, что ОМ = z, то ОА = 2z, AM = z
Q по условию - середина отрезка АМ, и значит, AQ = QM = z/2
Длина OQ
OQ = z + z/2 = 3/2 z
Треугольники OMK и OQS подобны с коэффициентом подобия 3/2
И длина QS составит
QS = 3/2·MK = 3/2·4 = 6
И это ответ.
Можно так же рассмотреть QS как среднюю линию трапеции AMKD, с тем же результатом.