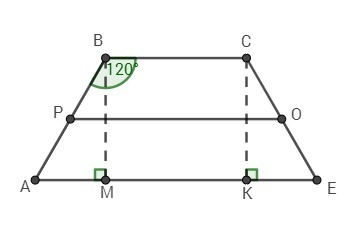
Пусть дана трапеция АВСЕ
АЕ || ВС
∠АВС = 120°
Решение:
основания трапеции не могут быть одинаковой длины, следовательно даны длины меньшего основания и боковых сторон:
АВ = ВС = СЕ = 6 см, значит трапеция равнобокая,
∠ВСЕ = ∠АВС = 120°
Опустим высоты ВМ и СК.
Высоты трапеции перпендикулярны основаниям ⇒ ВСКМ - прямоугольник, отсюда: МК = ВС = 6 см
Рассмотрим треугольники АВМ и ЕСК:
∠АВМ = ∠ЕСК = 120 - 90 = 30°
В прямоугольном треугольнике, катет, лежащий против угла 30° равен половине гипотенузы, отсюда:
АМ = АВ/2 = 6/2 = 3 см
КЕ = СЕ/2 = 6/2 = 3 см
АЕ = АМ + МК + КЕ = 3 + 6 + 3 = 12 см
Средняя линия трапеции равна полусумме оснований, отсюда:
РО = (ВС + АЕ)/2 = (6 + 12)/2 = 9 см
Ответ: 9 см.