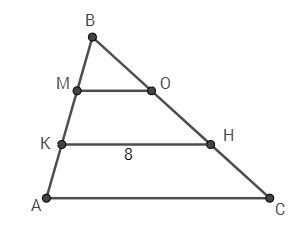
Пусть дан ΔАВС
АК = КМ = МВ
МО || KH || AC
КН = 8 см
Найти: АС
Из условия:
АК = КМ = МВ и МО || KH || AC, тогда, по теореме Фалеса:
СН = НО = ОВ
Следовательно, ΔАВС ~ ΔКВН
Пусть АК = КМ = МВ = х, тогда:
АВ = 3х
КВ = 2х
В подобных треугольниках соответствующие стороны пропорциональны, отсюда:

Ответ: 12 см.