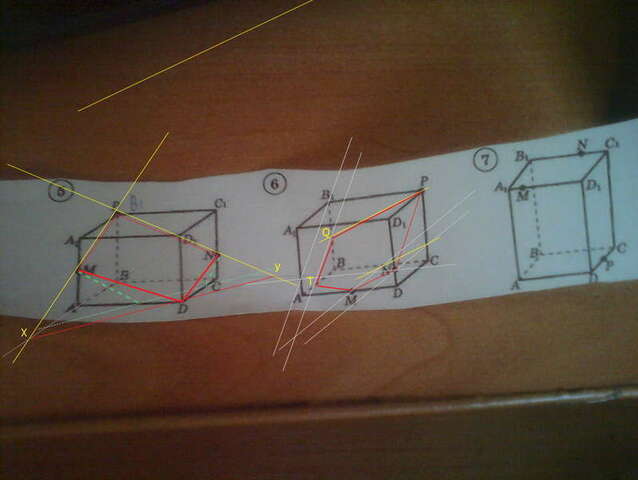
точки, лежащие
в одной плоскости просто
соединить прямой линией...
((прямую однозначно определяют 2 точки, плоскость --- 3 точки )))
соединяем РМ
соединяем PN
уже получилась плоскость PMN
эта плоскость пересекает грань АА1В1В по прямой РМ
и теперь важно представить ВСЮ
ПЛОСКОСТЬ АА1В1В (она ведь не ограничивается ребром АА1... и ребром АВ...)))
и тогда и у "прямой" РМ появится продолжение (это ведь НЕ отрезок --- это
прямая... здесь очень важно пространственное воображение...)))
аналогично и с прямой PN...
вверху эти прямые пересекаются в точке Р --- значит нам интересно посмотреть пересечение с плоскостями внизу... (представьте, что большим плоским ножом ((плоскостью...))) разрезается большой куб ((торт в форме куба...)))
осталось "разрезать" плоскости
AA1D1D
DD1C1C
ABCD (верхнее основание мы "задели" только в вершине В1 )))
теперь по порядку: плоскость AA1D1D...
ее визуальная граница --- ребро АВ (нас интересующее сейчас... А1В1 --- в верхнем основании и нас
не интересует... а точка М лежит на АА1...
значит мысленно продолжим АВ --- это ведь прямая линия, а не отрезок...))) и найдем точку пересечения РМ и АВ -------------------------
эта точка будет лежать и на боковой грани АА1В1В (вместе с прямой РМ) и на грани ABCD, т.к. АВ --- граница (визуальная) этих двух плоскостей --- линия их пересечения...
точно так же построим точку, лежащую и на ВВ1С1С и на ABCD
(продолжив ребро ВС --- как границу плоскости с прямой PN и плоскости ABCD...)))
получившиеся точки Х и У
обе лежат в плоскости ABCD
поэтому их можно соединить
прямой, лежащей
в этой плоскости...
и теперь нам нужно найти пересечение этой прямой и нужных плоскостей
AA1D1D
DD1C1C по их границам с ABCD...
здесь получилась одна точка D и поэтому сечение ---
четырехугольник PMDN
ЕСЛИ БЫ прямая в плоскости ABCD прошла чуть выше (я ее нарисовала зеленым пунктиром ---
только чтобы объяснить...))) ТОГДА сечением был бы пятиугольник...
словами объяснить сложнее, чем показать...
не знаю, смогла ли я быть понятной... но старалась...
ИТОГО: тремя точками определяется плоскость...
обычно для построения сечения три точки и указывают...
и дальше нужно искать пересечения заданных прямых
с ребрами многогранника... (ребра --- это визуальные границы плоскостей-граней, видимые линии их пересечения...)))))
во втором случае проще объяснить через параллельность противоположных граней... (это просто другой способ...)))
т.к. данный многогранник --- параллелепипед, то параллельным переносом построим точки М1 и N1 на грани ВВ1РС и прямая PQ будет параллельна M1N1
(((yна чертеже все точки и не обозначить... места не хватит...)))
аналогично QT || PN (т.к. параллельны содержащие их грани...)))
а Т и М уже просто соединяем, как лежащие в одной плоскости...
(((для пирамиды, например, строилось сечение бы иначе...)))
сомневаюсь, что понятно объяснила...