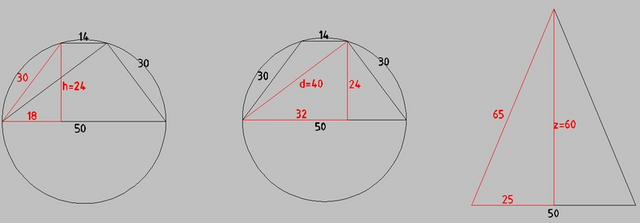
Три этапа решения. Я, правда, на рисунке сразу нарисовал описанную окружность трапеции.
1. Найдём высоту трапеции
рассмотрим треугольник, образованный боковой стороной, проведённой к основанию высотой и частью основания длиной (50-14)/2 = 36/2 = 18 см
По Пифагору
h²+18²=30²
h²=30²-18²=(30-18)(30+18)=12*48
h= √(12*48) = √(4*3*16*3)=2*3*4 = 24 см
2. Для нахождения радиуса описанной вокруг трапеции окружности надо найти диагональ трапеции. Тогда у нас будут длины сторон треугольников, на которые трапеция разбивается диагональю, и через эти длины по формуле Герона можно найти радиус описанной окружности
Рассмотрим треугольник, образованный диагональю, высотой и частью нижнего основания длиной 50 - (50-14)/2 = 50-18 = 32
Снова по Пифагору
d²=32²+24² = 1024+576 = 1600
d=√1600 = 40 см
Удача! Большой треугольник под диагональю имеет размеры 30,40,50 - это удесятирённый Египетский треугольник, прямоугольный. А в прямоугольном треугольнике диаметр описанной окружности совпадает с гипотенузой, а радиус описанной окружности равен половине гипотенузы, 50/2 = 25 см
3.
Переходим в вертикальную плоскость, рассматриваем сечение описанной окружности по большому основанию трапеции.
Равносторонний треугольник, боковые стороны которого 65, основание 50.
Для нахождения расстояния от точки до плоскости трапеции рассмотрим половинку этого равностороннего треугольника, с нива по Пифагору
z²+25²=65²
z²=65²-25² = (65-25)(65+25) = 40*90
z=√(40*90)=2*10*3 = 60 см
И это ответ :)