2a) По теореме синусов
AB/sin(∠C) = BC/sin(∠A)
6√2/sin(45°) = BC/sin(30°)
6√2/(1/√2)) = BC/(1/2)
6*2 = BC*2
BC = 6
2б) снова по теореме синусов
AB/sin(∠C) = BC/sin(∠A)
AB = BC*sin(∠C)/sin(∠A) = 8√3*sin(45°)/sin(60°) = 8√3*(1/√2)/(√3/2) = 8√2
2в) Сначала вычислим угол, противолежащий неизвестной стороне
∠B = 180°-∠A-∠C = 180°-30°-105° = 45°
А теперь по теореме синусов
AC/sin(∠B) = BC/sin(∠A)
AC = BC*sin(∠B)/sin(∠A) = 7*sin(45°)/sin(30°) = 7*(1/√2)/(1/2) = 7√2
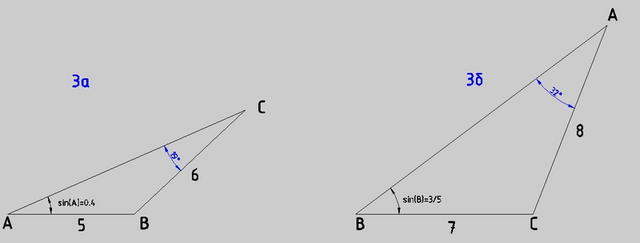
3a) опять теорема синусов
BC/sin(∠A) = AB/sin(∠C)
6/0,4 = 5/sin(∠C)
15=5/sin(∠C)
sin(∠C) = 1/3
3б)
AC/sin(∠B) = BC/sin(∠A)
8/(3/5) = 7/sin(∠A)
40/3 = 7/sin(∠A)
sin(∠A) = 7*3/40 = 21/40
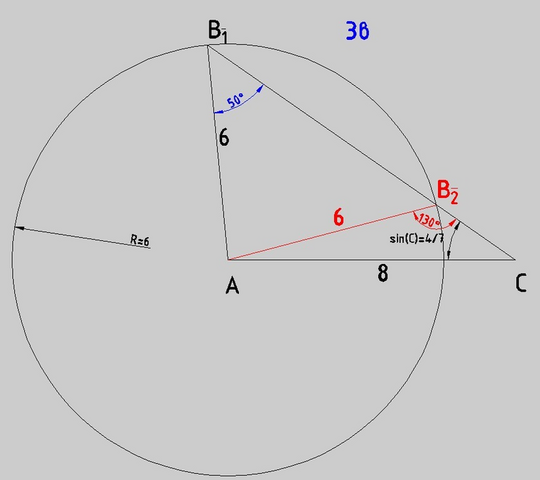
3b)
AB/sin(∠C) = AC/sin(∠B)
6/(4/7) = 8/sin(∠B)
3*7/2 = 8/sin(∠B)
sin(∠B) = 16/21
Решений два, но у каждого значение синуса именно такое.