Пронумеруем разряды числа номерами от 1 до N. Пусть три хода Игоря выделяют подмножества разрядов M₁, M₂ и M₃. Каждому разряду с номером k сопоставим тройку чисел s(k)=(a₁,a₂,a₃) по правилу 
, если 
и 
, если 
, где i=1,2,3. Назовем эту тройку сигнатурой разряда. Если для каких то двух разрядов c номерами k и m оказалось s(k)=s(m), то у Игоря нет никакой принципиальной возможности определить какая цифра в какой позиции находится. Поэтому количество цифр, которое может определить Игорь за 3 хода, не превосходит количества различных троек s(k), т.е. не превосходит 2³=8, и значит N≤8. И если Игорь хочет определять своими ходами максимальное количество разрядов, то ходы ему надо составлять так, чтобы каждой сигнатуре принадлежал только один разряд. и M₁∪M₂∪M₃ охватывало как можно больше разрядов. Если для какого-то разряда его сигнатура оказалась (0,0,0), т.е. этот разряд вообще не был затронут ходами Игоря, то определить цифру в этом разряде невозможно, т.к. цифр всего 10 и 10>8. Т.е. Игорь может определять цифры только в тех разрядах, которые принадлежат M₁∪M₂∪M₃. Значит N≤7. Покажем, что при N=7 множества M₁, M₂ и M₃ можно выбрать так, что каждой сигнатуре будет принадлежать только один разряд, и значит 7 цифр Игорь сможет всегда определить, например, с помощью следующих ходов:
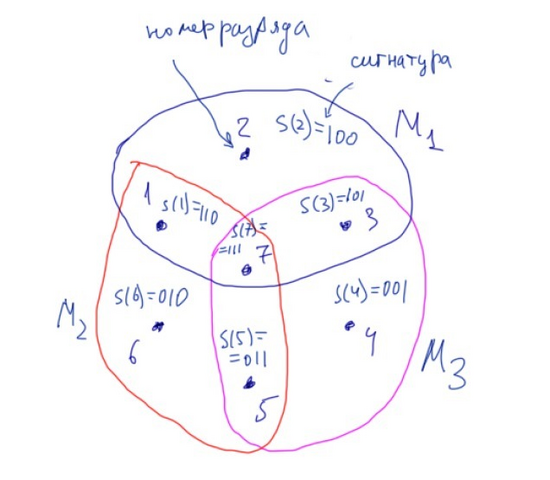
M₁={1,2,3,7}, M₂={1,5,6,7}, M₃={3,4,5,7} (см. рисунок).
В ответе Миши будут названы цифры, стоящие в разрядах с соответствующими номерами.
Тогда та цифра, которая будет фигурировать во всех трех ответах Миши, находится в 7-ом разряде, т.к. s(7)=111 и с такой сигнатурой этот разряд единственный.
Та цифра, которая будет фигурировать в 1-ом и 2-ом, но не в 3-м ответе Миши находится в разряде с номером 1 (см. рисунок), т.к. s(1)=110 и опять, с этой сигнатурой имеется только один разряд.
Цифра, которая будет фигурировать, например в 3-м ответе Миши, но не в 1-ом и не во 2-ом, соответствует позиции 4, т.к. s(4)=001 и т.д. Итак, по ответам Миши мы определяем сигнатуру каждой упомянутой цифры (смотрим, в каких ответах эта цифра есть, а в каких ее нет), и поскольку сигнатура однозначно связана с номером разряда, мы определяем позицию этой цифры.
Заметим, что если бы число было записано в восьмеричной системе счисления, то Игорь мог бы определить все цифры при N=8, т.к. определив семь позиций у него оставалась бы одна не задействованная цифра на 8-ую позицию.
