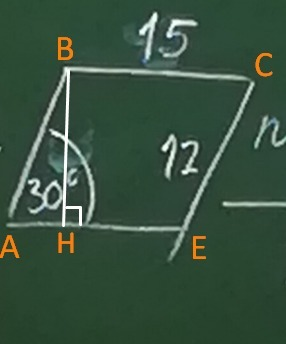
Пусть дан параллелограмм АВСЕ
ВС = 15
СЕ = 12
∠BAE = 30°
Найти: S
Противоположные стороны параллелограмма равны, отсюда:
АВ = СЕ = 12
АЕ = ВС = 15
Опустим высоту ВН к стороне АЕ.
ΔАВН - прямоугольный
В прямоугольном треугольнике катет, лежащий против угла 30°, равен половине гипотенузы, отсюда:
ВН = АВ/2 = 12/2 = 6
Площадь параллелограмма равна произведению его основания на высоту:
S = AE * BH = 15 * 6 = 90 ед²