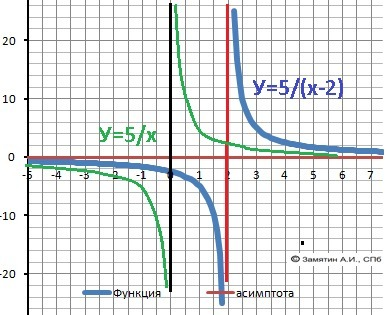
ДАНО
Y = 5/(2-x)
РЕШЕНИЕ
1. Область определения. В знаменателе не должно быть 0.
(2 - х) ≠ 0 и х≠2. Разрыв функции - вертикальная асимптота: x = 2
X∈(-∞;2)∪(2;+∞)
2.Горизонтальная асимптота - поведение на бесконечности.
lim(-∞)Y(x)= 0, lim(+∞) Y(x) = 0.
Горизонтальная асимптота: Y = 0.
3. Проверка на чётность.
Y(-x) = 5/(2+x) ≠ Y(x).
Функция ни чётная ни нечётная.
4. Дополнительные точки.
х = 2, у = 5/1 = 5
х = - 3, у = -1
5. График функции в приложении.
Дополнительно.
График можно построить сдвинув базовый график У=5/х вправо на 2.