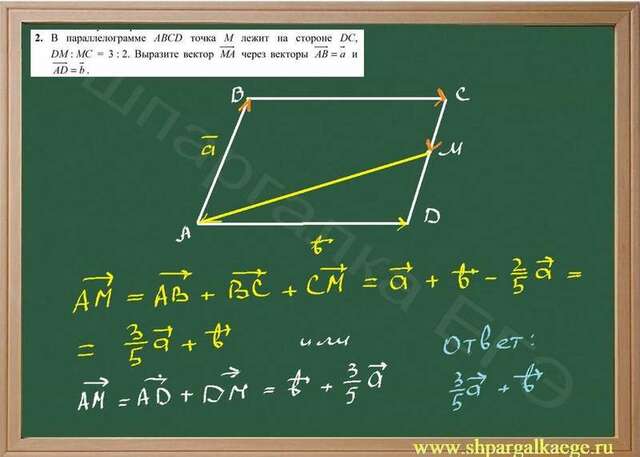
Данный урок показывает, как через известные вектора в виде боковых
сторон параллелограмма, выразить произвольный отрезок в виде композиции
исходных векторов. Данная задача не могла бы иметь решения, если бы мы
не знали, в каком соотношении делится одна из сторон параллелограмма
точкой , принадлежащей искомому отрезку. Дальнейшие действия сводятся к
определению начала и конца заданных векторов и векторов, на который
делится боковая сторона. Все это необходимо, чтобы правильно
использовать знаки при комбинации векторов. Ведь необходимо помнить
правила сложения векторов: сумма векторов дает третий вектор, начало
которого совпадает с началом первого вектора, а конец с концом второго; и
правило вычитания векторов: разность двух векторов – третий вектор,
начало которого совпадает с концов второго вектора, а конец с концом
первого вектора. Исходя из этих простых правил, можно получить
необходимую нам комбинацию.
Решение данной задачи рекомендовано для учащихся 8-х классов при
изучении темы «Вектора» («Понятие вектора. Задачи», «Сложение и
вычитание векторов», «Умножение вектора на число. Применение векторов к
решению задач»).