Найти точку разрыва функции и определить ее тип. Начертить схематический график функции в...

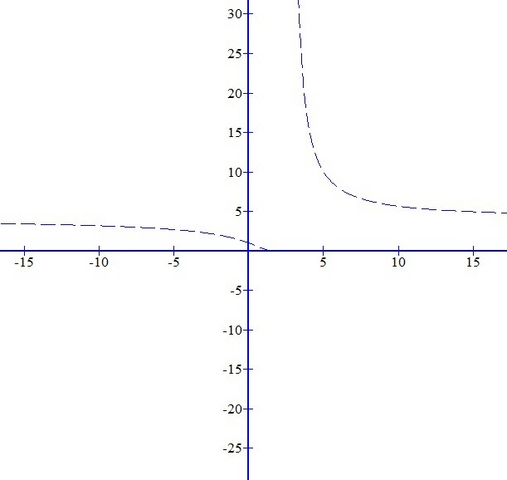
Из выражения степени при 4 видно, что в точке x = 2 функция не определена. Найдём левый и правый пределы функции в этой точке:

$\lim_{x \to 2+0} 4^{ \frac{x}{x-2}} = \lim_{x \to 2+0} 4^{ \frac{2}{+0}} = 4^{\infty} = \infty$

$\lim_{x \to 2-0} 4^{ \frac{x}{x-2}} = \lim_{x \to 2-0} 4^{ \frac{2}{-0}} = 4^{-\infty} = 0$

Один из пределов равен бесконечности, поэтому точка - точка разрыва второго рода. График функции с точкой разрыва на картинке.