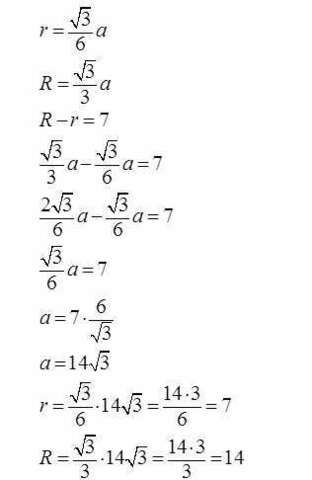Можно
и без формул! Тогда решение становится совсем простым!
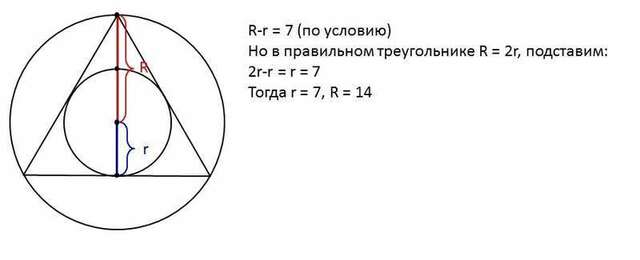
В правильном треугольнике центры вписанной и описанной окружностей совпадают. Центр
вписанной лежит на точке пересечения биссектрис треугольника, но в правильном
треугольнике каждая из биссектрис является и медианой, следовательно, центр
вписанной и описанной окружностей правильного треугольника – это и точка
пересечения медиан этого треугольника. Медианы, пересекаясь, делятся как 2:1,
считая от вершины треугольника. Получается, на радиус описанной окружности
приходится две части, на радиус вписанной – одна часть, радиус описанной окружности равен двум
радиусам вписанной R = 2r.
Разница между ними R – r = 2r – r = r = 7 см. То есть, 7 см
и есть радиус вписанной окружности! Тогда радиус описанной окружности в два
раза больше – это 14 см.
Прилагаю чертёж, по которому станет понятно.
Если с использованием формул, то смотрите на втором приложенном
изображении. Формулы для R и r через сторону
правильного треугольника известны.