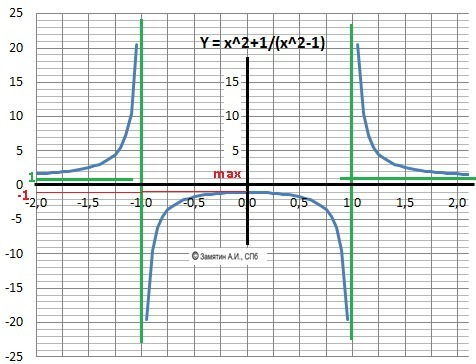
ДАНО
Y(x)
= (x2+1)/(х2-1)
1.Область
определения D(x).
(х2-1)
= (х-1)*(х+1)=0.Функция неопределена при х= +/- 1.
Вертикальные
асимптоты: х = -1 и х =1.
2.
Пересечение с осью Х. Y=0 - нет.
Положительна
- X∈(-∞;-1)∪(+; +∞), отрицательна - X∈(-1;1).
3. Пересечение
с осью У. У(0) = (02+1)/(02 -1) = -1.
4. Поведение
на бесконечности.limY(-∞) =1, limY(+∞) =1
Горизонтальная
асимптота Y=1
5.
Исследование на чётность.Y(-x) = Y(x).
Функция
чётная.
6.
Производная функции –
Y'(x)=
2*x/(x²-1) -2x(x²+1)/(x2-1)2.
Корень: Х=0.
7.
Локальные экстремумы. Максимум Ymax(0)= -1.
8.
Интервалы возрастания и убывания.
Возрастает
- Х∈[-∞;-1] ∪[-1;0), убывает = Х∈(0;1]∪[1;+∞).
8.
Вторая производная - Y"(x) = -6*x=0.
Действительных
корней - нет .
Точки
перегиба в точках разрыва функции.
9.
Выпуклая “горка» Х∈(-1;1).
10.
График в приложении.