1) Преобразуем данную функцию:

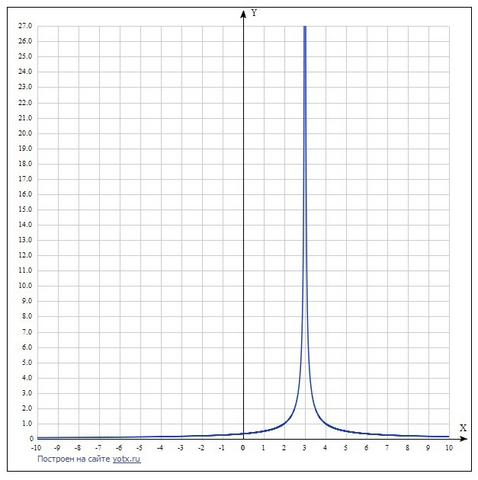
2) Строим график (он получится из графика y=1/|x| путём сдвига вправо по оси Ох на 3 единицы (см. график в приложении)
3) Теперь легко можно определить множество значений функции.
Это интервал (0;+∞)
Ответ: E(y)=(0;+∞)
*** Если требуется ещё и область определения, то это объединение интервалов D(y)=(-∞;3)U(3;+∞)