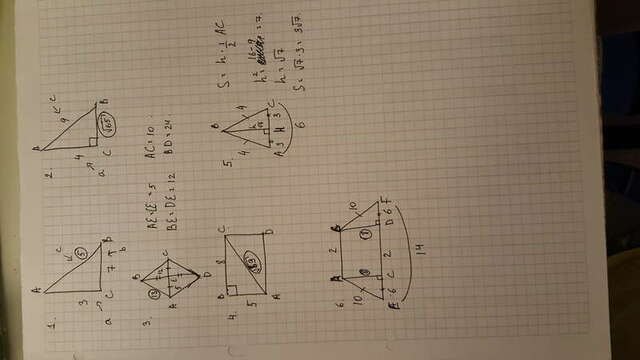
1. Найдем гипотенузу по формуле: c^2 = a^2 + b^2, где c - квадрат гипотенузы, a и b - катеты. c^2 = 3^2 + 7^2 = 9 + 14 = 25. Обратим внимание на то, что мы нашли квадрат гипотенузы. Чтобы получить ответ нужно найти корень полученного значения: с = sqrt25 = 5. Ответ: 5.
2. Найдем катет по формуле: a^2 = c^2 -
b^2. a^2 = 9^2 - 4^2 = 81 - 16 = 65. a = sqrt65 (так и оставляем, т.к. целого корня у 65 нет). Ответ: корень из 65.
3. Т.к. у ромба диагонали равны, то каждую диагональ делим на 2. Поделив, можем найти сторону ромба через теорему Пифагора, где сторона - гипотенуза.
10:2 = 5; 24:2 = 12. - катеты.
c^2 = 5^2 + 12^2 = 25 + 144 = 169.
c = sqrt169 = 13. Ответ: 13.
4. Тоже решаем по теореме Пифагора, где диагональ - гипотенуза.
c^2 = a^2 + b^2.
c^2 = 8^2 + 5^2 = 64 + 25 = 89.
c = sqrt89. Ответ: корень из 89.
5. Площадь равнобедренного треугольника равняется произведению высоты на половину длины основания.
Проведем высоту. Поделим основание на 2: 6:2 = 3. Зная половину основания и сторону равнобедренного треугольника, можем найти высоту по теореме Пифагора, где высота - катет.
a^2 = c^2 - b^2.
a^2 = 4^2 - 3^2 = 16 - 9 = 7.
a = sqrt7.
Найдем площадь: S = h * AC/2, где h - высота, AC - основание.
S = sqrt7 * 6/2 = 3* sqrt7. Ответ: 3*корень из 7.
6. Проведем в трапеции высоты. Пусть AB - верхнее основание, EF - нижнее основание. Проведя высоты, получим: AC - высота, BD - высота. Видим, что трапеция состоит из одного прямоугольника и двух прямоугольных треугольников, при этом ABCD - прямоугольник. Зная, что у прямоугольника стороны параллельно равны, получим: AB = CD = 2.
Далее, из нижнего основания 14 вычитаем 2. Получаем 12. Это число нужно поделить на 2. 12:2 = 6 - нижние катеты прямоугольного треугольника.
Зная боковую сторону и нижний катет, можем найти высоту по теореме Пифагора, где высота - катет.
a^2 = c^2 - b^2.
a^2 = 10^2 - 6^2 = 100 - 36 = 64.
a = sqrt64 = 8.
Ответ: 8.