Уравнение не имеет корней, если дробь в левой части не определена (знаменатель равен нулю) или если значение дроби в правой части неположительно.
Первый случай: знаменатель равен нулю.
5 - a = 0
a = 5
Второй случай: дробь <= 0<br>(2a + 3) / (5 - a) <= 0<br>(2a + 3) / (a - 5) >= 0
Метод интервалов. числитель обращается в ноль при a = -2/3, знаменатель при a = 5. Знак "+" будет при a <= -2/3 и при a > 5:
++++++++++++ [-2/3] -------------------- (5) ++++++++++++++++ → a
Ответ. при a <= -2/3 и при a >= 5.
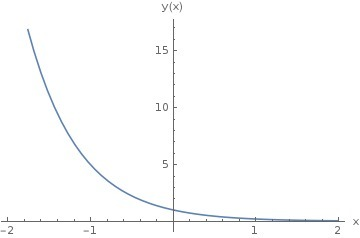
В приложении график функции y=0.2^x, на котором видно, что функция может принимать любое положительное значение.