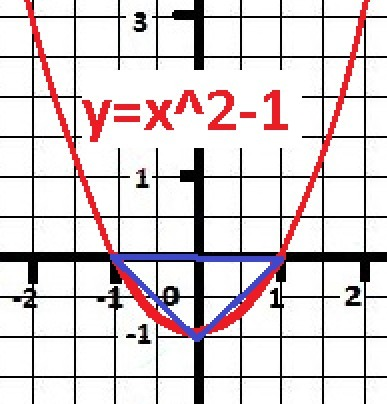
Уравнение квадратного трехчлена можно привести к виду:
Y = a*x² - b = (x² - b/a) = (x - √c)*(x + √c)
где: b - вершина параболы, с = b/a, +/- √c - корни трехчлена - точки пересечения с осью Х.
Треугольник - прямоугольный.Это значит что катеты равны: √c = b.
√(b/a) = b, b/a = b² ,
b = 1/a - условие прямоугольного треугольника.
При а = 1, b = 1, √c = 1.
Гипотенуза треугольника
d = √с - (-√с) = 1- (-1) =2 - ОТВЕТ
Рисунок к задаче в приложении.