В прямоугольном треугольнике ABC с катетами AB=10, AC=24 проведены медианы AM и CN, M и N...

Question

В прямоугольном треугольнике ABC с катетами AB=10, AC=24 проведены медианы AM и CN, M и N -- середины сторон BC и AB -- соответственно. Точка I лежит на стороне AC, при этом BI - биссектриса. Найдите площадь треугольника MNI

Answer 1

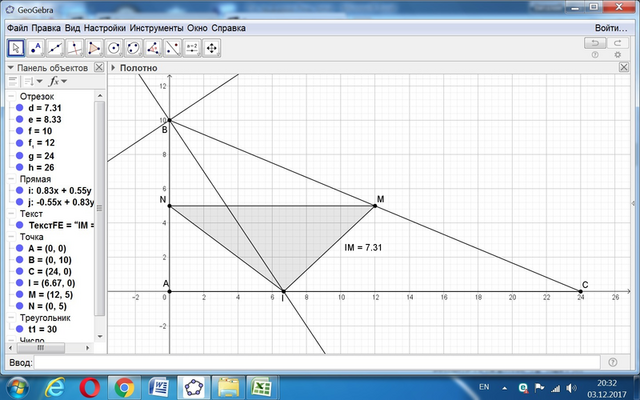
Находим ВС = √(10² + 24²) = √(100 + 576) = √676 = 26.
Находим отрезок AI по свойству биссектрисы:
AI = (24/(26 + 10))*10 = 20/3.
Теперь находим длины сторон треугольника  MNI.
Отрезок MN как средняя линия равен 24/2 = 12.
NI = √(5²+(20/3)²) = √(25+(400/9)) = √(625/9) = 25/3.
MI = √(5² + (12 - (20/3))²) = √(481/9) ≈ 7,310571.
Искомую площадь треугольника  MNI находим по формуле Герона:
S = √(p(p-a)(p-b)(p-c)). Полупериметр р = 13,821952.
Подставив данные в формулу, находим S = 30.

---