Означення. Прямокутник — це паралелограм, у якого всі кути прямі.
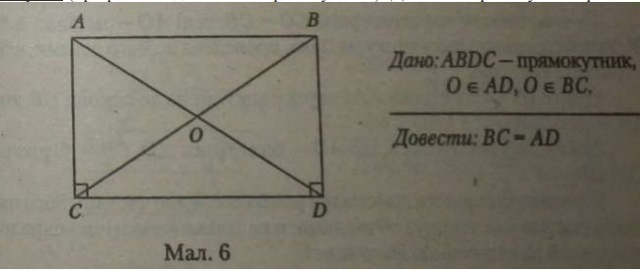
Теорема (про рівність діагоналей прямокутника). Доведення. Для доведення використовуємо той факт, що ∆ACD=∆ВCD за
першою ознакою рівності трикутників (CD — спільна, АС= BD як протилежні
сторони паралелограма, C= D=90). А в рівних трикутниках проти рівних
кутів (у цьому випадку прямих кутів) лежать рівні сторони.
Отже, ВС=AD, як гіпотенузи рівних прямокутних трикутників, ще й необхідно
було довести.
Властивості прямокутника
1. Протилежні сторони рівні й паралельні.
2. Усі кути прямі.
3. Діагоналі рівні, перетинаються в одній точці і точкою перетину діляться
пополам.
4. Кожна діагональ ділить прямокутник на два рівні трикутники.
5. Точка перетину діагоналей є спільною вершиною чотирьох трикутників, які
попарно рівні і мають в основах паралельні прямі.