ДАНО
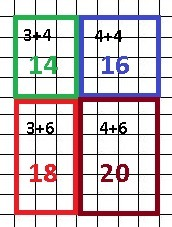
Р₁=14, Р₂=16, Р₃ = 18 - периметры 3 частей
НАЙТИ
Р₄ =? - периметр четвертой части.
Добавим к условию задачи, что разделен он двумя прямыми линиями, как на рисунке в приложении.
Вариант решения - геометрия и арифметика.
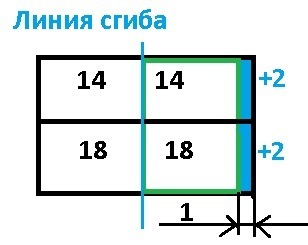
Рисунок 2. Согнем лист по вертикальной линии деления прямоугольника.
После наложения получим, что прямоугольник с периметром 16 выступает снизу на 1 ед. (По формуле: х= (Р₂ - Р₁)/2 = (16-14)/2=1)
На такую же величину выступает и нижний прямоугольник с периметром Р₃=18.
Получаем - периметр четвертого равен Р₄ = 18+2 = 20 см - ОТВЕТ
Вариант 2. -
Используя формулу периметра прямоугольника Р = 2*(a+b) приходим к выводу, что нам надо найти общие числа в сумме
a+b = 7, a+c =8 и d+b =9.
Искомый периметр - Р₄ = 2*(d+c)
В целых числах это может быть: a=4, b=3, c=4, d=6
P₄ = 2*(4+6) = 20.
ОТВЕТ: Периметр = 20.