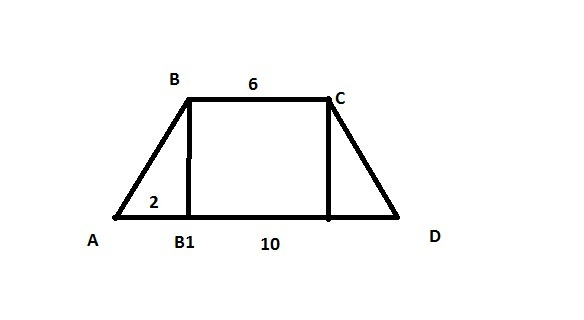
Для начала найдем боковую сторону трапеции
AB1=(AD-BC)/2=(10-6)/2=2
AB=AB1/sin30=2*2=4
Надо найти высоту BB1^2=AB^2-AB1^2=16-4=12
BB1==2√3
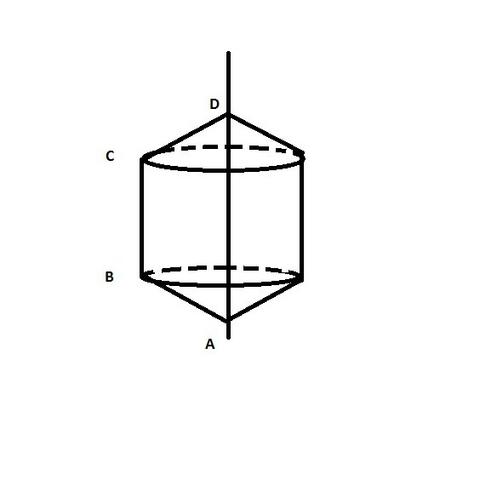
решим без интегралов, вся площадь поверхности состоит из 3 частей, 2 одинаковых конусообразных поверхностей S1 снизу и сверху и цилиндрической посередине S2
S2=2pi*BB1*BC=2*2√3*6*pi=24√3 pi
S1=pi*BB1*AB=pi*2√3*4=8√3pi
Тогда общая площадь поверхности
S=2S1+S2=2*8√3pi+24√3pi=40√3pi