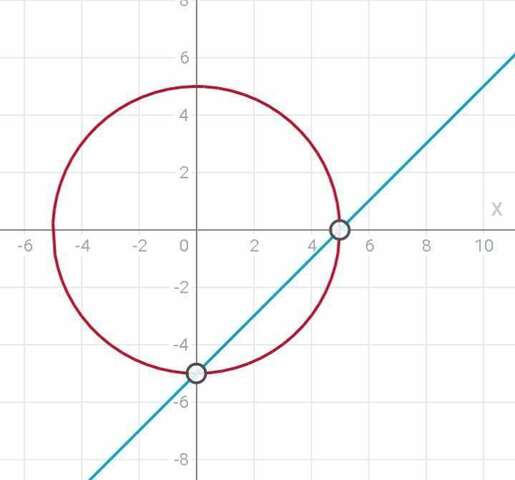
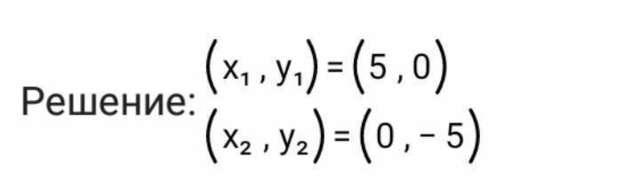Номер 3,номер 4:
пусть х первое число,тогда у-второе .
составим систему уравнение:
х^2-y^2=100
3x-2y=30
х=30+2у/3
х=10+2/3 у
100+40/3 у + 4/9 у^2 -y^2-100=0
-5y^2+120 y =0
-y (5y-120)=0
y1=0-не подходит
5y-120=0
y2=24
х2=10+2*24/3=26
Ответ:26 и 24 ископаемые числа
5 номер;
Решение:
y= x^2+4, x^2+(x^2+4)^2 =k или х^4+9x^2+16=k или (x^2+4,5)^2-4,25=k, Далее проfнализируй при k=4,5, k<4,5, k>4,5