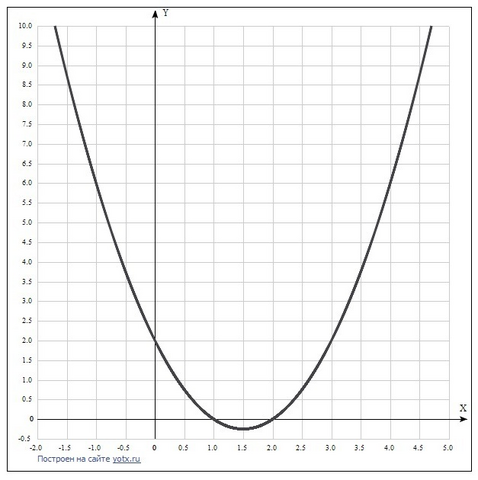
График функции y = x² - 3x + 2 это парабола ветвями вверх.
Находим координаты её вершины.
хо = -в/2а = 3/2 = 1,5.
уо = 1,5² - 3*1,5 + 2 = 2,25 -4,5 + 2 = -0,25.
1) область определения и область значений.
Область определения функции D(f) = R.
Область значений функции Е(f) = [-0,25; +∞).
2) интервалы возрастания и убывания.
Функция убывает: х ∈ (-∞; 1,5),
возрастает х ∈ (1,5; +∞).
3) нули функции находим, приравняв функцию нулю:
x² - 3x + 2 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-3)^2-4*1*2=9-4*2=9-8=1;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√1-(-3))/(2*1)=(1-(-3))/2=(1+3)/2=4/2=2;x_2=(-√1-(-3))/(2*1)=(-1-(-3))/2=(-1+3)/2=2/2=1.
Получаем 2 точки пересечения графиком оси Ох:
(2; 0) и (1; 0).