Вообще,
уравнение 4-ой степени решается сперва формулой Феррари, а затем формулой
Кордано, но здесь можно поступить иначе.
4-ай степень
говорит, что уравнение имеет 4 корня.
В данном
уравнении можно найти корни, а затем
разделить уравнение на них.
Чаще всего корнями таких уравнений является делитель
члена n (aх⁴+bх³+cх²dх+n=0)
При чем при
делении n на корень чаще всего получается цело число.(Не путай! Корень не
Обязательно будет целый! При делении n на корень должно получится целое число!)
В данном
случае это число 8. Его делителями будут числа 1, 2, 4 ,8, -1, -2, -4,-8, 1/2, 1/4, 1/8, -1/2, -1/4 и -1/8.
Первым корнем будет
число 2 (при желании вы можете подставить и проверить)
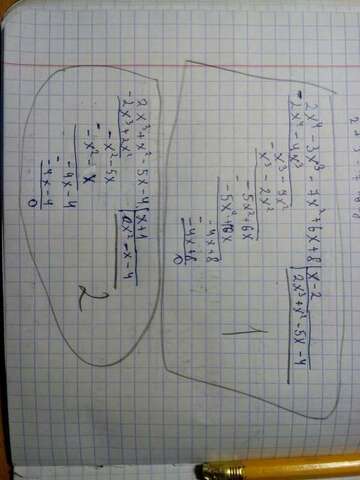
При делении на этот корень
получаем уравнение вида 2х³+х²-5х-4 (деление уравнениq приложу отдельно).
Далее таким же способом
ищем тут корень. Вторым корнем является число -1.
При делении 2х³+х²-5х-4
на этот корень получаем уравнение вида 2х²-х-4=0, корни которого находятся
через дискриминан и равны (1+√33)/4 и (1-√33)/4. Уравнение Решено.
Ответ: 2;-1; (1+√33)/4 и (1-√33)/4.