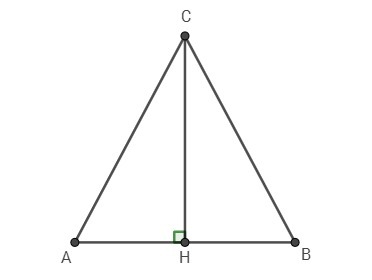
Дано:
ΔАВС
АС = ВС
АВ = 16
Р(АВС) = 50
Найти: S(ABC)
АС = (50 - 16)/2 = 17
Опустим высоту СН. В равнобедренном треугольнике высота, опущенная к основанию, является также медианой ⇒ АН = АВ/2 = 16/2 = 8
В ΔАСН (∠АНС = 90°) по теореме Пифагора:
СН = √(АС² - АН²) = √(17² - 8²) = √225 = 15
S(ABC) = (АВ*СН)/2 = (16*15)/2 = 120 ед².