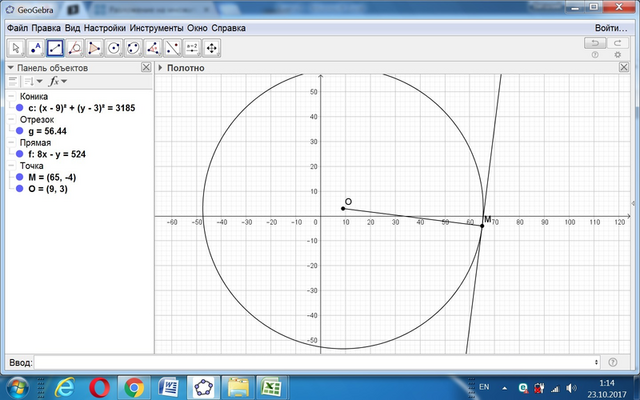
Центр окружности - точка О(9; 3). Точка М(65; -4).
Уравнение ОМ: (х - 9)/(65-9) = (у - 3)/(-4-3),
(х - 9)/56 = (у + 3)/(-7).
В общем виде: -7х + 63 = 56у - 168,
7х + 56у - 231 = 0, сократим на 7:
х + 8у - 33 = 0.
В виде с коэффициентом: у = (-1/8)х + (33/8).
Касательная в точке М имеет к = -1/(-1/8) = 8.
Её уравнение у = 8х + в.
Найдём в, подставив координаты точки М:
-4 = 8*65 + в,
в = -4 - 520,
в = -524.
Ответ: уравнение касательной у = 8х - 524.