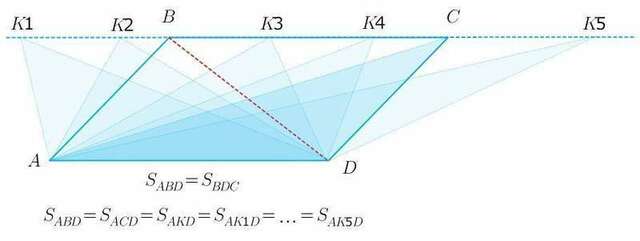
Площади треугольников, имеющих равные основания и равные высоты, равны.
если в параллелограмме провести диагонали, то площади треугольников ABD и ACD будут равны и =половине площади параллелограмма...
а эти треугольники НЕ равны (один остроугольный, другой тупоугольный)
высоты параллелограмма, проведенные из вершины В и из вершины С равны... и если они (высоты) будут проведены из любой точки на стороне ВС --они все будут равны...
вывод: если построить треугольник с основанием, равным стороне параллелограмма (AD) и вершиной, лежащей в любой точке на параллельной основанию стороне параллелограмма (BC), то всегда получатся равновеликие треугольники (с равными площадями) и это будет площадь половины параллелограмма.
т.е. S(BPA) = 0.5*S
MP--медиана (по условию) треугольника ВРА
медиана делит треугольник на два равновеликих треугольника.
S(AMP) = S(BMP) = 0.5*0.5*S = 0.25*S = S/4