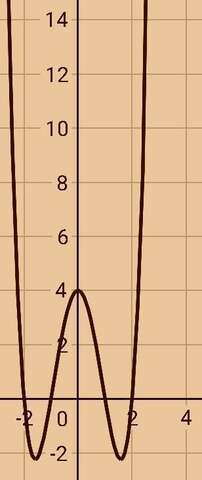
Решение (график прилагается):
(x-2)(x-1)(x+1)(x+2)=40
Упростим выражение:
(x^2-4)(x^2-1)=40
Перемножим скобки:
x^4-x^2-4x^2+4=40
Снова упростим выражение:
x^4-5x^2=36
С помощью корня квадратного решить эту фразу:
x=(-(-5)+-√(-5)^2-4*1*(-36))/(2*1)
Упростить выражение:
x=(5-13)/2
Найти x:
x^2=9
x^2=-4
=> [x1=-3
[x2=3
Ответ: x=+-3.