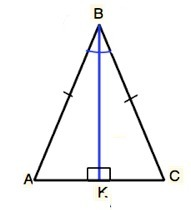
В ∆ АВС стороны АВ=ВС, ВК - биссектриса.
Рассмотрим ∆ АВК и ∆ СВК.
АВ=ВС, ВК - общая, угол АВК=СВК. ⇒ Треугольники равны по первому признаку: по двум сторонам и углу, заключенному между ними.
Из равенства треугольников ∆ АВК и ∆ СВК следует МК=СК⇒
ВК - медиана ∆ АВС.
В равных треугольниках углы, противолежащие равным сторонам, равны. ⇒
∠ВКА=∠ВКС
АКС – развернутый угол и равен 180°.
ВК делит его на два равных с градусной мерой 180°:2=90° ⇒
ВК⊥АС и является высотой равнобедренного треугольника АВС.