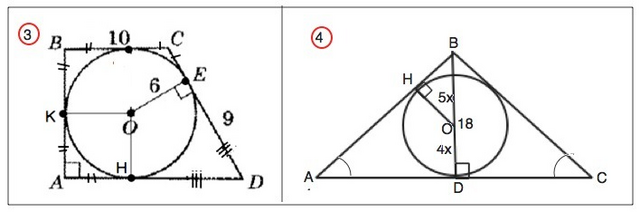
3. На рис.133 АВСD -трапеция, точка О – центр вписанной окружности, ОЕ=6см, ВС=10 см, DE=9 см. Найдите периметр трапеции.
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. (свойство).
ОЕ⊥СD⇒ ОЕ - радиус.
АВ⊥ВС и АD
Проведем OK⊥АВ
ОК=r
OH⊥AD
АН=ОК=OE=6
HD=ED=9
AD=AH+HD=15
Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.
Трапеция - четырехугольник.
ВС+AD=AB+CD
Р=ВС+AD+AB+CD=2•(10+15)=50 см
——————————————————
4. На рис. 134 точка О – центр вписанной окружности, угол А=углу С, BD=18 см, BO:OD=5:4. Найдите стороны треугольника.
DO+ВО=9х ⇒
х=18:9=2
OD=8, ВО=10.
По условию углы при АС равны. ⇒ ∆ АВС - равнобедренный, АВ=ВС.
Центр вписанной в треугольник окружности лежит на биссектрисе.
Биссектриса равнобедренного треугольника - высота и медиана. ⇒
∠BDA=90°
AD=CD.
Проведем ОН - перпендикуляр в точку касания на АВ.
Из ∆ ВОН по т.Пифагора ВН=6
В прямоугольных ∆ АВD и ∆ OBH острый угол при В общий.⇒
∆ АВD~∆ OBH
Из подобия следует отношение
АВ:ВО=ВD:BH
AB•6=10•18⇒
AB=180:6=30
По т.Пифагора AD=24 ⇒
АС=48
ВС=АD=30