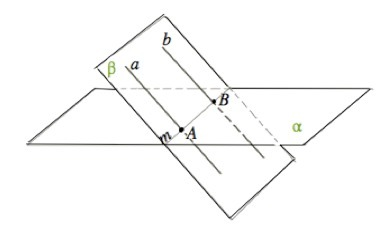
Дано: а и b параллельные прямые, и прямая а пересекает плоскость α.
Обозначим точку пересечения а и плоскости буквой А.
Известно, что через две параллельные прямые можно провести плоскость, притом только одну. Пусть это будет плоскость β.
Прямая а лежит в плоскости β, точка А принадлежит прямой а, значит, А тоже принадлежит плоскости β. Точка А лежит в плоскости α и в плоскости β.
Если две плоскости имеют общую точку, то они имеют общую прямую, которая является линией пересечения этих плоскостей ( аксиома).
Обозначим общую прямую плоскостей α и β буквой m. Прямые a, b и m находятся в плоскости β
Если на плоскости одна из параллельных прямых пересекает какую либо прямую, то вторая прямая тоже пересекает эту прямую.
Точку пересечения прямых b и m обозначим B
Так как точка B находится на прямой m,то точка B находится в плоскости α и является единственной общей точкой прямой b и плоскости α.
.Следовательно, прямая b пересекает плоскость α.