Фигура, заданная ** координатной плоскости двойным неравенством 0=<x^2 +y^2–2y=<9 ,...

Question

Фигура, заданная на координатной плоскости двойным неравенством

0=

(x+1–y)( ax√3+y–1)=0 , на несколько частей. Найдите наибольшее число a , при котором площадь наименьшей части относится к площади наибольшей части как 5:7 . РЕШЕНИЕ и КАРТИНКУ.

ЕРУНДУ НЕ ПИШИТЕ. УДАЛЯЮ СРАЗУ.

---

---

Answer 1

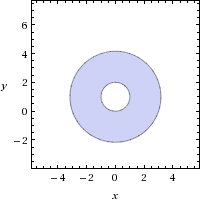
Найдите наибольшее число a  , при котором площадь наименьшей части относится к площади наибольшей части как 5:7 

0= 1=

(x+1–y)( ax√3+y–1)=0 <=> системе y=x+1, y=1--a√3x

Обе прямые проходят через центр кольца , т.е. через точку (0;1). Поэтому отношение площадей частей, на которые делят прямые кольцо, равно отношению соответствующих углов между прямыми.

-a√3=tg2pi/3 <=>-a√3=-√3 <=> a=1

ЧАСТЬ I

ЧАСТЬ II

СМ. ВО ВЛОЖЕНИИ

Ответ  a=1

 

 

---