Егэ математика профиль

Question

Дан 1 ответ

SkipperF_zn · Answer 1 · 2018-05-17T17:31:30+0000

$\left(x+\dfrac{3}{x}\right)\cdot\bigl(\log_{5-x}(x^2-6x+9)\bigr)^2\geqslant4\cdot\bigl(\log_{5-x}(x^2-6x+9)\bigr)^2 \\ \\ \left(x+\dfrac{3}{x}\right)\cdot\Bigl(\log_{5-x}\bigl((x-3)^2\bigr)\Bigr)^2\geqslant4\cdot\Bigl(\log_{5-x}\bigl((x-3)^2\bigr)\Bigr)^2 \\ \\ \left(x+\dfrac{3}{x}\right)\cdot\Bigl(2\log_{5-x}\bigl|x-3\bigr|\Bigr)^2\geqslant4\cdot\Bigl(2\log_{5-x}\bigl|x-3\bigr|\Bigr)^2 \\$

Переносим всё в левую часть:

$\left(x+\dfrac{3}{x}\right)\cdot\Bigl(2\log_{5-x}\bigl|x-3\bigr|\Bigr)^2-4\cdot\Bigl(2\log_{5-x}\bigl|x-3\bigr|\Bigr)^2\geqslant0 \\ \\ \Bigl(2\log_{5-x}\bigl|x-3\bigr|\Bigr)^2\cdot\left(\left\Bigl(x+\dfrac{3}{x}\Bigr)-4\right)\geqslant0 \\$

Множитель, который положителен при всех значениях $x$ из области определения, можно отбросить. При этом не забудем про ОДЗ и про случай, когда этот множитель равен нулю. (Так как неравенство нестрогое.)

Найдём ОДЗ:

$\begin{cases} & 5-x\ \textgreater \ 0 \\ & 5-x\neq1 \\ & |x-3|\ \textgreater \ 0 \\ & x\neq0 \end{cases}\; \Leftrightarrow \; \begin{cases} & x\ \textless \ 5 \\ & x\neq4 \\ & x\neq3 \\ & x\neq0 \end{cases}$

На области определения(!) наше неравенство равносильно совокупности двух условий:
1)
$2\log_{5-x}\bigl|x-3\bigr|=0 \\ \log_{5-x}\bigl|x-3\bigr|=0 \\ \log_{5-x}\bigl|x-3\bigr|=\log_{5-x}1 \\ |x-3|=1 \\ x_1=4, \ x_2=2$

2)
$x+\dfrac{3}{x}-4\geqslant0 \\ \\ \dfrac{x^2-4x+3}{x} \geqslant0 \\ \\ \dfrac{(x-3)(x-1)}{x} \geqslant0 \\$
Решая это неравенство методом интервалов, получаем: $0\ \textless \ x\leqslant1$ или $x\geqslant3$ .

В итоге мы получили систему из ОДЗ и совокупности:
$\begin{cases} & x\ \textless \ 5 \\ & x\neq4 \\ & x\neq3 \\ & x\neq0 \\ & \left[ \begin{gathered} \left\ \begin{gathered} x=4\\ x=2\\ 0\ \textless \ x\leqslant1\\ x\geqslant3\ \end{gathered} \right. \hfill \\ \end{gathered} \right. \end{cases}$

После нахождения пересечения множества допустимых $x$ и множества решений получаем ответ:
$0\ \textless \ x\leqslant 1$ , или $x=2$ , или $3\ \textless \ x\ \textless \ 4$ , или $4\ \textless \ x\ \textless \ 5$ .
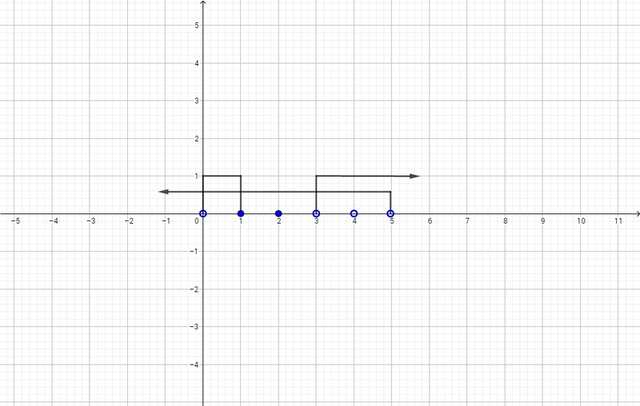
Или, что то же самое, но в другой форме:
$x \in(0;1]\cup\{2\}\cup(3;4)\cup(4;5)$ .