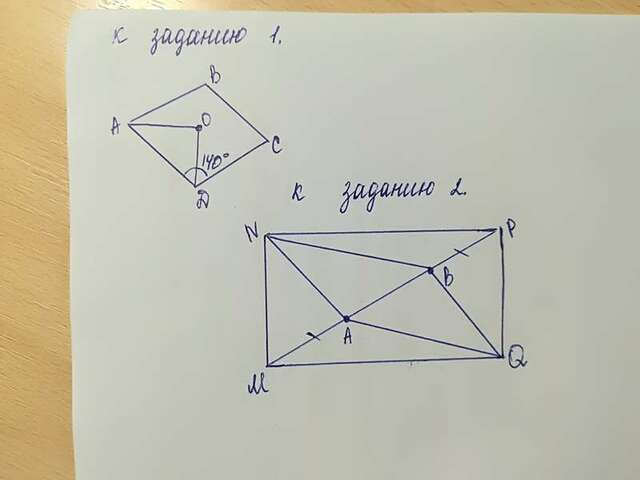
1.
В ΔAOD ∠O = 90°, т.к. диагонали ромба пресекаются под прямым углом.
∠ODA = 70°, т.к. диагонали делят углы ромба пополам.
Значит, ∠DAO = 180-(90+70) = 20°
Ответ: 20° ; 70° ; 90°.
2.
Рассмотрим ΔPBN и ΔMAQ. (они = по 2-м сторонам и ∠ между ними):
PN = MQ (как противоположные стороны прямоуг.)
BP = AM (по условию)
∠NPM = ∠QMP (как накрест лежащие ∠ при пересечении 2-х параллельных прямых PN и MQ секущей MP. ⇒ AQ = BN.
Рассмотрим ΔPBQ и ΔMAN. (они = по 2-м сторонам и ∠ между ними):
PQ = MN (как противоположные стороны прямоуг.)
BP = AM (по условию)
∠QPM = ∠NMP (как накрест лежащие ∠ при пересечении 2-х параллельных прямых MN и PQ секущей MP. ⇒ BQ = AN.
Применив признак параллелограмма о том, что если в четырёхугольнике противоположные стороны попарно = (AQ = BN и BQ = AN), то этот четырёхугольник - параллелограмм ⇒ ANBQ - параллелограмм.