Помогите пожалуйста решить, срочно нужно f(x) = x3/3-3x2+5x-7, [-1, 3]Зарание, спасибо)))

Question

Помогите пожалуйста решить, срочно нужно f(x) = x3/3-3x2+5x-7, [-1, 3]
Зарание, спасибо)))

Answer 1

F(x) = x³/3-3x²+5x-7, [-1, 3]
x³/3-3x²+5x-7=0
x³=3(3x²-5x+7)
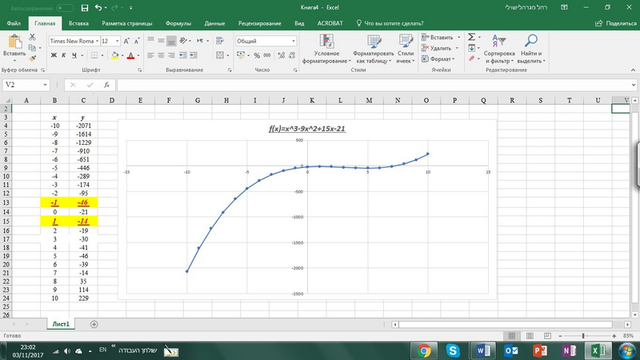
f(x)=x³-9x²+15x-21
f`(x)(3x³-9x²+15x-21)=3x²-18x+15=3(x²-6x+5)
x²-6x+5=0
D=36-4*5=16
x₁=1
x₂=5
Критические точки: х₁=1,x₂=5
x₁=1∈[-1,3]
x₂=5∉[-1,3]
f(x₁)=f(1)=1³-9*1²+15*1-21=-14
f(-1)=(-1)³-9*(-1)²+15*(-1)-21=-46
f(3)=3³-9*3²+15*3-21=-30
Ответ: max f(x)=f(1)=-14
            [-1,3]
            min f(x)=f(-1)=-46
            [-1.3]
     Прилагаю график

---