1.
а) Функция корня 3 степени - монотонно возрастающая, значит, данная нам функция y(x) - монотонно убывающая. Из этого следует, что в точке {-8} значение наибольшее, а в точке {0} - наименьшее.
б) x^2+1 - монотонно возрастающая. Это значит, что с данной нам монотонно убывающей функцией точка пересечения ровно одна.
Чтобы найти ее, нужно решить уравнение![- \sqrt[3]{x}+1=x^2+1 - \sqrt[3]{x}+1=x^2+1](https://tex.z-dn.net/?f=-+%5Csqrt%5B3%5D%7Bx%7D%2B1%3Dx%5E2%2B1+)
Легко убедиться подбором, что 0 - корень этого уравнения. Значит, точка пересечения только в нуле, т.к. она всего одна.
2.
Область определения - множество, которое задается следующими неравенствами:

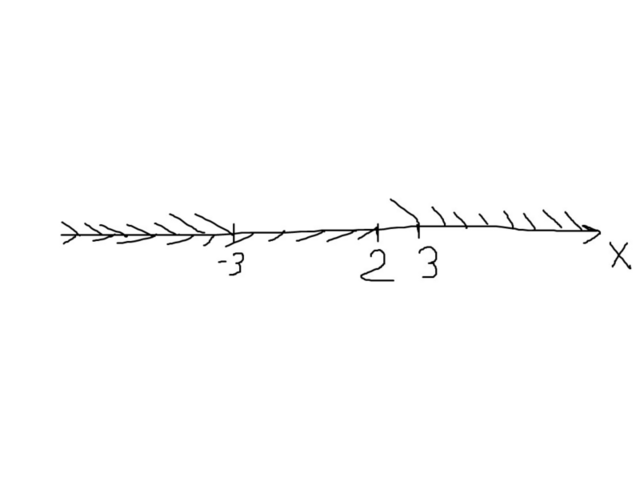
Из первой очень криво нарисованной картинки видно, что область определения - ![(-\infty;-3] (-\infty;-3]](https://tex.z-dn.net/?f=%28-%5Cinfty%3B-3%5D)
3.
Наибольшее и наименьшее значения функции корня будут в точках наибольшего и наименьшего значений подкоренного выражения соответственно (при этом подкоренное выражение не может быть меньше нуля). А областью значений будет отрезок от наименьшего до наибольшего этих значений. Нетрудно убедиться, что подкоренное выражение достигает нуля, т.к. это парабола направленная вниз. Значит, наименьшее значение функции это 0. Наибольшее значение будет достигаться в пике параболы: 
![\sqrt[4]{48+2*1-1^2}=\sqrt[4]{49}=\sqrt{7} \sqrt[4]{48+2*1-1^2}=\sqrt[4]{49}=\sqrt{7}](https://tex.z-dn.net/?f=+%5Csqrt%5B4%5D%7B48%2B2%2A1-1%5E2%7D%3D%5Csqrt%5B4%5D%7B49%7D%3D%5Csqrt%7B7%7D)
Значит, область значений будет ![[0;\sqrt{7}] [0;\sqrt{7}]](https://tex.z-dn.net/?f=%5B0%3B%5Csqrt%7B7%7D%5D)