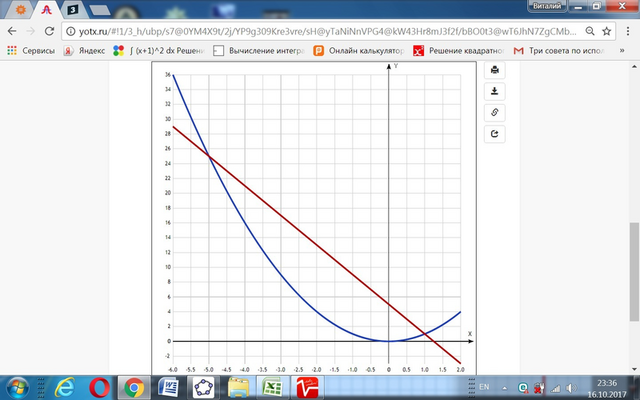
Координаты точек пересечения графиков функций y=x² и y=5-4x определяются совместным решением этих уравнений:
x²=5-4x,
х² + 4х - 5 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=4^2-4*1*(-5)=16-4*(-5)=16-(-4*5)=16-(-20)=16+20=36;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√36-4)/(2*1)=(6-4)/2=2/2=1;x₂=(-√36-4)/(2*1)=(-6-4)/2=-10/2=-5.
у₁ = 1² = 1,
у₂ = (-5)² = 25.
Ответ: точка А(1; 1), точка В(-5; 25).
сумма абсцисс точек пересечения равна 1-5 = -4.