Решение первого на листе.
Решение второго(см. рисунок на втором фото):
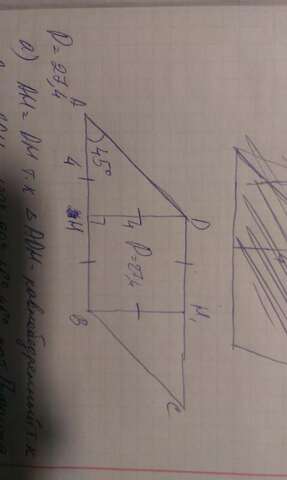
Высота DH=4, 45'-острый угол, пусть это будет угол A. Тогда треугольник ADH - равнобедренный. => DH=AH. AH=HB по условию. => AH=HB=4, a) AB=AH+HB, AB=8=DC.
P=27.4, P=AB+BC+CD+AD. AD=BC=x=8, AB=DC=y.
P=2x+2y; 27.4=16+2y; y=(27.4-16)/2; y=5.7=AD=BC.
Ответ: AD=BC=5.7 , AB=DC=8.
б) Проведём диагональ DB, высоту BH1.
BH1=DH - это высоты. Мы получаем прямоугольник DH1BH, который является квадратом, т.к. все его стороны равны. Мы получаем равные прямоугольные треугольники DH1B и DHB. По двум сторонам и углу между ними треугольник DHB= треугольнику ADH. Тогда AD=DB=5.7.