Надо решить показательное уравнение: 3ˣ⁻⁵ + 4ˣ⁻⁵ = 91

Question

Надо решить показательное уравнение:

3ˣ⁻⁵ + 4ˣ⁻⁵ = 91

Comments

3^(x-5) или 3^x^(-5)

---

думаю так 3^(x-5)

---

х=8

---

подобрать и я могу

---

х - 5 - это показатель

Answer 1

Я рассуждал так.
Изначально можно установить что х>5, т.к. при х<5 значение <img src="https://tex.z-dn.net/?f=3%5E%7Bx-5%7D+" id="TexFormula2" title="3^{x-5} " alt="3^{x-5} " align="absmiddle" class="latex-formula"> и  стремятся к нулю, а значит равенство не будет выполняться. Так же значение  или  не могут быть по отдельности равны 91 (максимальным целым показателем степени для 3 является 4, для 4 является 3). То есть показатель степени находится в пределах   5P.S. Очевидно, что показателем степени будет целое число.

Comments

А при помощи Диофантового уравнения?

Answer 2

Теорема. 1) Если на некотором промежутке функция f(x) возрастает (или убывает), то  уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).

- возрастающая, как сумма возрастающих функций.

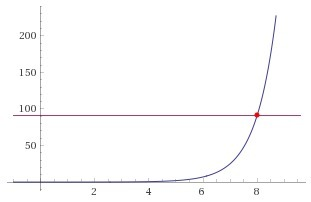
f(x) = 91

Эти две графики пересекаются в одной точке, то есть, по теореме выше сказанному, уравнение имеет единственное решение и его найти можно путем подбора.

Ответ: х=8.

---