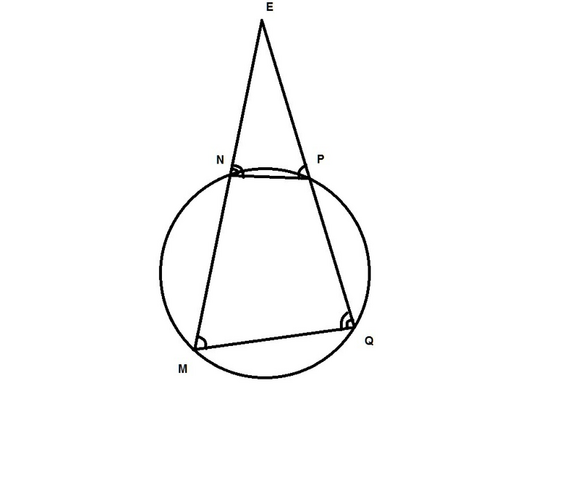
Если четырехугольник вписан в окружность, то сумма его противоположных углов равна 180°
∠M+∠P=180°
∠N+∠Q=180°
1)
∠QPN+∠NPE=180° как смежные углы
∠M+∠NPQ=180° ⇒ ∠M=∠NPE
2)
∠MNP+∠PNE=180° как смежные углы
∠Q+∠MNP=180° ⇒ ∠Q=∠PNE
3)
∠E у треугольников ENP и EQM общий
Следовательно, ΔENP подобен ΔEQM по трем углам, что и требовалось доказать.